Indexing and slicing in numpy
Indexing and slicing in numpy:
Indexing and slicing in numpy is similar to indexing and slicing in lists.
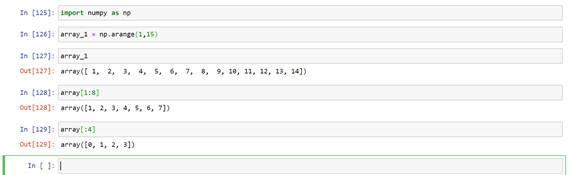
Here challenges come when the array is two dimensional, Let us see indexing in two dimensional array.
There are two ways to access an element from 2D array.
– array_1[2][3]
– array_1[2,3]

Second method should be preferred as it is easier.
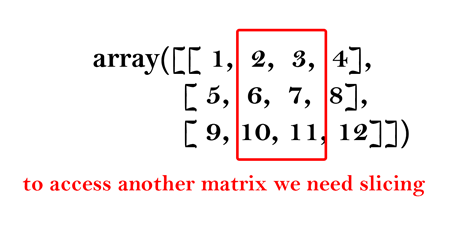
To access this matrix from the bigger matrix
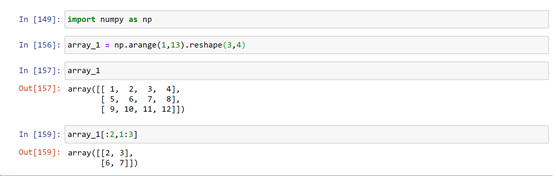
array_1[:2,1:3]
: 2 This means selecting rows from beginning to 2nd row
1:3 This means selecting column from 1st to 3rd index positions.
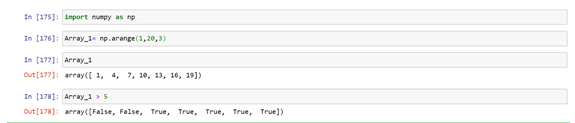
Conditional Selection:
In python when we compare two integers in return we get Boolean expression, But in array we don’t have single element in it to get Boolean expression.
Array_1 = np.arange(1 ,20,3 )
Array_1 > 5 # what do we get in return let us check
All the elements of the array get compared with the scalar value and we get another array of Boolean expressions.
When we pass the conditional statement in a array, then we get an array of the elements , which satisfies the confition. This is Conditional Selection.
Operations with arrays:
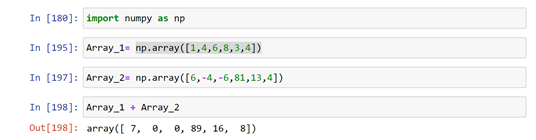
- Array addition with array: We can add two arrays by placing + sign between two arrays, A condition is that the two array should have same shapes. Then the elements with same positions will be added.
- Array Multiplication:

- Array division:

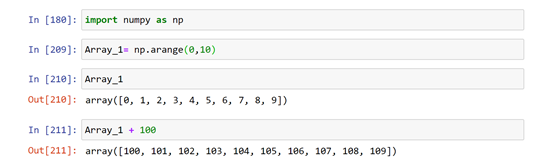
- Array addition with scalar : In this operation each element of the array is added to the scalar element.
- Array Multiplication with scalar:

- Array division with scalar:

Universal array functions:
- np.sqrt ( array_name ) : This function gives the square root value of all the elements of the array passed in the function.
- np.sin(array_name) : This function gives the sine of the elements.

There are such many number of universal function that are available.
Over all at the end of numpy tutorial we can say that , In these tutorials many manipulations were similar to Matlab, with this we can say that Numpy has a potential to replace matlab in mathematical and logical operations.
